排序算法-nlogn篇

在众多的排序算法中，我们往往根据不同的需求选择不同的排序算法，从时间复杂度的角度考虑，排序算法中的时间复杂度O(nlogn)是一个算法复杂度较好，且常见的算法策略。

​ 本篇文章，我们来讨论排序算法中的具有O(nlogn)时间复杂度的排序算法。

一、合并排序

1、基本思想

​ 合并排序，本质上是采用了分治的策略。所谓分治，即分而治之，将一个复杂的问题分成两个小部分，再对两个小部分分别求解，最后将两个解合并起来得到最终的解。

​ 合并排序的分治策略也很简单。将一个长度为n的序列分成若干部分（本文一般默认为两部分），对这两个部分分别做排序，最后对两个已经排好序的序列结果进行合并。当然，对于分开的两个部分，最理想的情况是分开的这个序列长度为1，这样已经是排好序的。为此，我们采用递归思想，当长度不为1的时候，我们持续分裂成两部分，直至长度为1。

2、基本流程

此处为算法基本流程：

if(长度是否为1)

​ 如果不为1，找到序列中点位置 i

​ 对序列最左端到中点 i 的位置的序列递归排序

​ 对序列 i+1 的位置到序列最右端的序列递归排序

​ 最后将两个排好序的两个部分合并成一个序列

​ 将结果拷贝到原序列中

算法实例如下图所示。

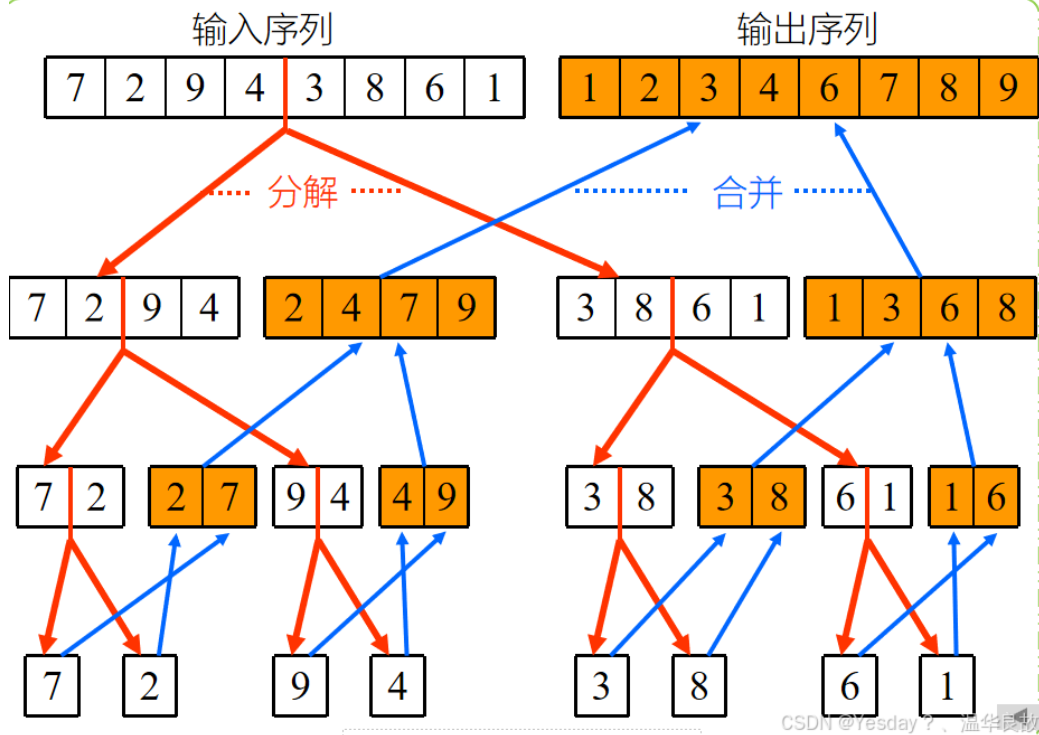
3、代码实现（C++）

void merge(int* arr, int left, int mid, int right);

void Process(int* arr, int left, int right)
{
	if (left == right) {
		return;
	} //如果数组长度为1,直接返回空
	int mid = left + ((right - left) >> 1); //求中点
	Process(arr, left, mid); //递归调用，左段排序
	Process(arr, mid + 1, right); //递归调用，右段排序
	merge(arr, left, mid, right); //合并两段
}

void merge(int* arr, int left, int mid, int right)
{
	int* help = new int[right - left + 1]; 
	int i = 0;
	int p1 = left;
	int p2 = mid + 1;
	/*
	比较两个数组当前位置，小的部分那个放入临时数组，两者后移一位
	直到有一方全部进入临时数组
	*/
	while (p1 <= mid && p2 <= right) 
		help[i++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++]; 
	//将有剩余的一方全部放入临时数组
	while (p1 <= mid)
		help[i++] = arr[p1++];
	while (p2 <= right)
		help[i++] = arr[p2++];
	for (int j = 0; j < right - left + 1; j++)//拷贝到原始数组
		arr[j + left] = help[j];
}

4、时间复杂度分析

在分析之前，我们需要了解一个著名的master公式：

T(N) = aT(N/b) + O(N^d)

• a: 计算的次数
• b: 子过程的个数
• O(N^d)：子过程合并的时间复杂度

满足如上公式的程序都可以根据master公式计算时间复杂度：

• log(b，a) > d ：时间复杂度为O(N^log(b，a))
• log(b，a) = d ：时间复杂度为O(N^d * logN)
• log(b，a) < d ：时间复杂度为O(N^d)

对于合并算法而言：

我们将一个数组分成两个部分，即对两个子过程排序，所以b等于2，

每个子过程都计算一遍，两个为2，所以a等于2，

在合并过程中，在前三个while循环中，我们一共对整个数组元素都扫描了一遍，所以复杂度的系数，则为O(N)，所以d=1。

显然合并排序满足上述公式，log(b,a) = d = 1，所以最后的时间复杂度是O(NlogN)。

5、相关题目

（1）小和问题

在一个数组中，每一个数左边比当前数小的数累加起来，叫做这个数组的小和。求一个数组的小和

例如：[1,3,4,2,5] 1左边比1小的数，没有；3左边比3小的数，1；4左边比4小的数，1,3；2左边比2小的数，1；5左边比5小的数，1,3,4,2；所以小和为16。

• 思路：从另一个角度思考该例子。1的右边有4个比1大的数，所以1计算了4次，41 = 4；3右边有2个比3大的数，3计算了2次，32 = 6；4右边有1个比4大的数，4计算了1次，14 = 4；2右边有1个比2大的数，计算1次，12 =2；5右边也没有，为0；最后总和为16。

• 代码

  int mergeOfSum(int* arr, int left, int mid, int right);
  int ProcessOfSum(int* arr, int left, int right)
  {
  	if (left >= right)
  		return 0;
  	int mid = left + ((right - left) >> 1);
  	return ProcessOfSum(arr, left, mid) +
  		ProcessOfSum(arr, mid + 1, right) + 
  		mergeOfSum(arr, left, mid, right);
  }
  
  int mergeOfSum(int* arr, int left, int mid, int right)
  {
  	int* help = new int[right - left + 1];
  	int i = 0;
  	int p1 = left;
  	int p2 = mid + 1;
  	int res = 0;
  	while (p1 <= mid && p2 <= right) {
  		res += arr[p1] < arr[p2] ? (right - p2 + 1) * arr[p1] : 0;
  		help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
  	}
  	while (p1 <= mid) {
  		help[i++] = arr[p1++];
  	}
  	while (p2 <= mid) {
  		help[i++] = arr[p2++];
  	}
  	return res;
  }

  

二、快速排序

1、基本思想

快速排序（Quicksort）是一种高效的排序算法，它也同样采用分治法（Divide and Conquer）策略来把一个列表分成较小的子列表，然后递归地排序这些子列表。

但与合并排序不同，合并排序是将两个排好序的子序列合并成一个序列，快速排序是选择一个基准，将小于基准的所有元素放在基准的左边，大于基准的所有元素放在基准的右边，然后对基准的两边分别重新选择基准排序。

从整体上，合并排序是将大部分拆成很多小部分，给小部分排好序，最后还要合成大部分。 快速排序是将大部分拆成小部分，在拆的过程中向着排好序的结果前进，全部拆完，顺序也就排好了。

2、基本流程

1. 选择一个基准（Pivot）：
   • 从待排序的序列中选择一个元素作为基准。选择基准的方法有多种，常见的包括选择第一个元素、最后一个元素、中间元素或随机选择一个元素。
2. 分区（Partitioning）：
   • 重新排列序列，使得所有比基准小的元素都位于基准的左侧，而所有比基准大的元素都位于基准的右侧（基准在其最终的排序数组中的正确位置）。
   • 经过分区操作后，基准的位置就已经固定，不再需要参与后续的排序。
3. 递归排序子序列：
   • 递归地对基准左侧和右侧的子序列进行快速排序，直到每个子序列的长度为0或1（已经有序）。

Partition过程，即在分区的过程，找到基准在序列中的位置，分成基准的左半区和右半区。

​ 其原理如下：

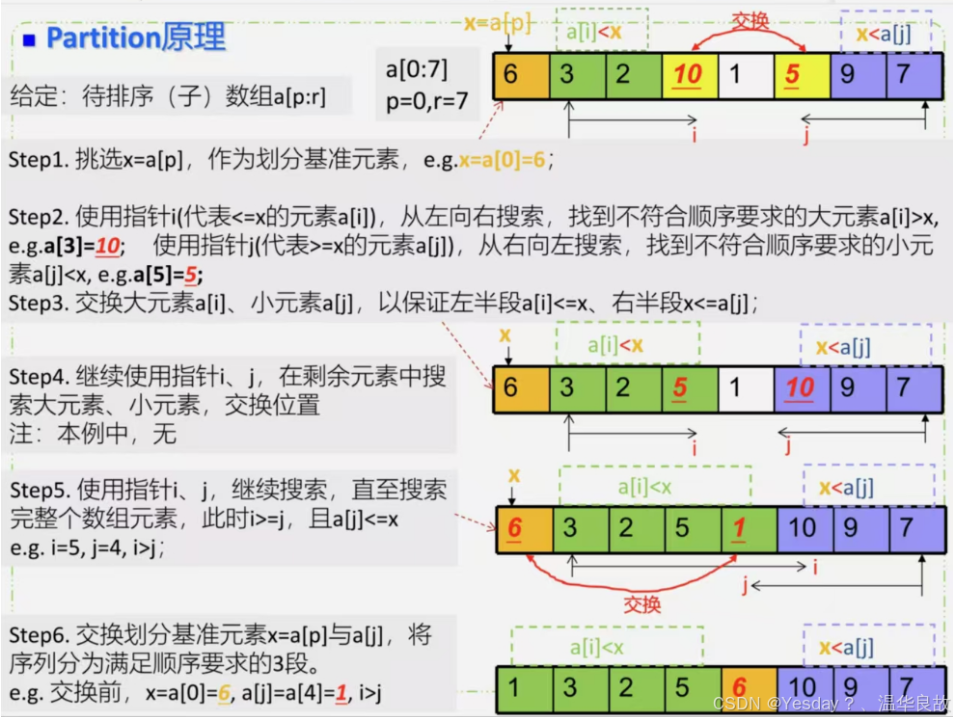
为了直观，我们对上图做出一个简练的原理总结：

• 选择基准如图第一个位置，为6。
• 用两个指针分别指向第二个头和尾，即6（头）和7（尾）
• 先处理尾部指针，如果指针指向的值大于基准值，跳过；如果小于或等于则记录此时尾指针的位置，我们可以看到，此时指向的是5。
• 头指针反过来，找到比基准值大于等于的值为止，记录此时头指针位置，此时指向的是10。
• 我们交换5和10的值即可。如此操作，直到头尾指针相遇为止，此时退出循环
• 在头尾指针相遇位置，即指向1的位置和基准值（序列首位置）交换，即6和1交换。
• 最终我们看到比基准值6小的都在左半区，比基准值6大的都在右半区，Partition结束，返回头尾指针相遇的位置。

3、代码实现（C++）

void quickSort(int* nums, int left, int right) {
	if (left >= right) //递归到底直接返回
		return;

	int pivot = partition(nums, left, right); //找到基准位置，分为左右两块分别作排序

	quickSort(nums, left, pivot - 1);  //左部分排序
	quickSort(nums, pivot + 1, right); //右部分排序
}


int partition(int* nums, int left, int right)
{
	int i = left;
	int j = right;

	while (i < j) {
		//注意两个循环顺序不能换，先让j--找到比基准数小的，这样无论i++能否找到比基准数大的，最后如果i==j跳出循环后进行交换仍能确保和基准数交换的数小于等于基准数
		while (i < j && nums[j] >= nums[left])
			j--;

		while (i < j && nums[i] <= nums[left])
			i++;
		swap(nums[i], nums[j]);
	}

	swap(nums[j], nums[left]);
	return j;
}

4、时间复杂度分析

T(N) = aT(N/b) + O(N^d)

在本例中，a等于2，b等于2，d等于1

log(b,a) == d

所以时间复杂度为 O(N^d * logN) = O(N*logN)

三、堆排序

1、基本思想

堆的定义：

堆heap是一种数据结构，是一棵完全二叉树且满足性质：所有非叶子结点的值均不大于或均不小于其左、右孩子结点的值，称之为小根堆或大根堆。

举个栗子：

​ 看过杯赛的同学应该都知道（世界杯、欧冠杯赛等等），如16支队伍相当于初始的叶子结点，经过两两的比拼，选出更厉害的8支队伍，依次比拼下去，始终更厉害的队伍晋级，最终两支决胜队伍比拼出冠军。将这整个过程用树状结构记录下来，用队伍的强度表示值，构成了一棵完全满二叉树，也是一个大根堆。

2、基本流程

基本流程主要分为两部分，分别为建堆和调整堆（本文主要按照大根堆来讲）。

建堆：按照树的层次遍历顺序，一次放入一个数到指定位置，放入一个数，跟自己的父节点作比较，如果发现比父节点大，就和父节点交换顺序，交换顺序后，如果还有父节点，继续比较，直到不比父节点大或者已经交换到根节点的位置为止，如下图所示。

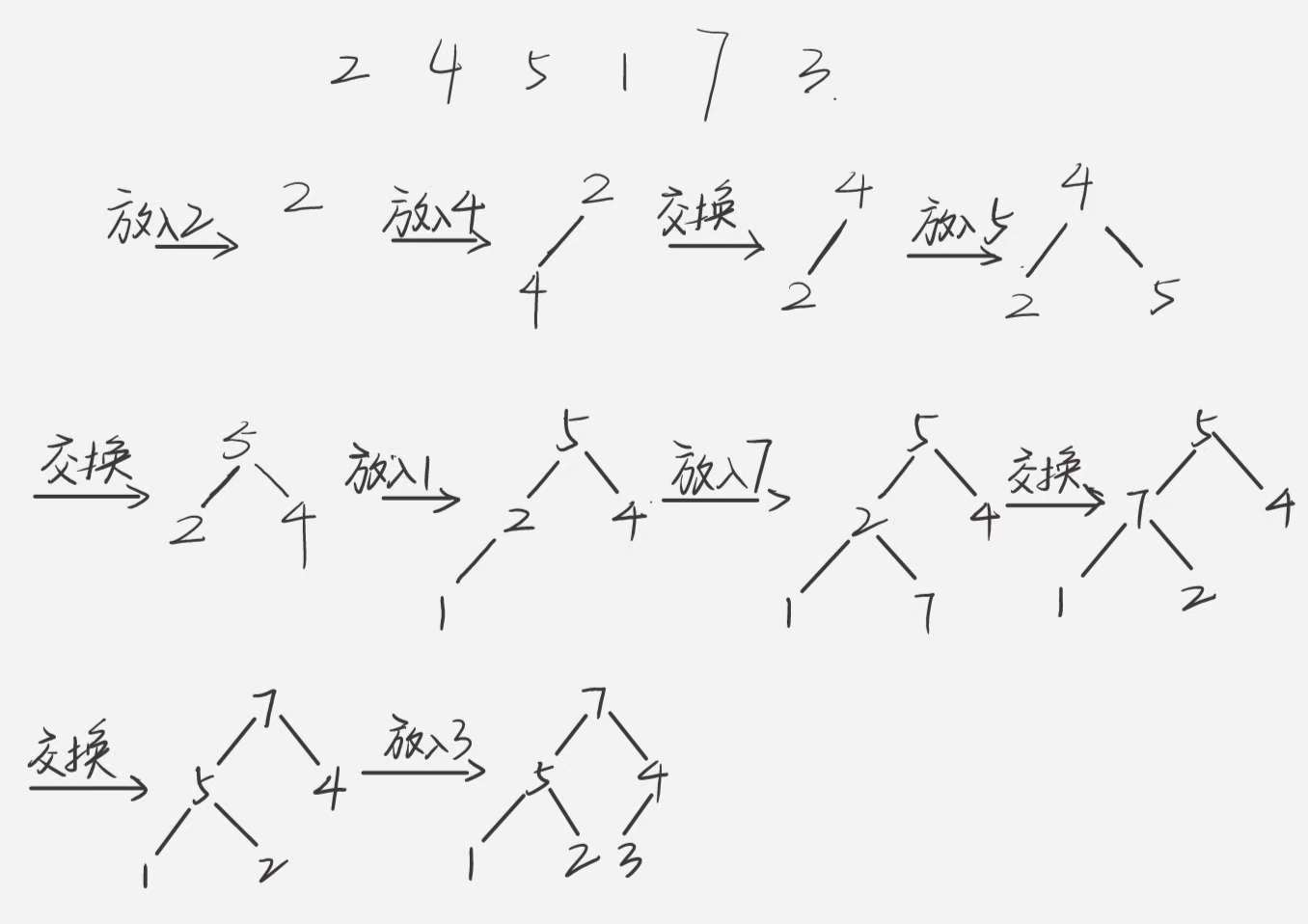
调整堆：

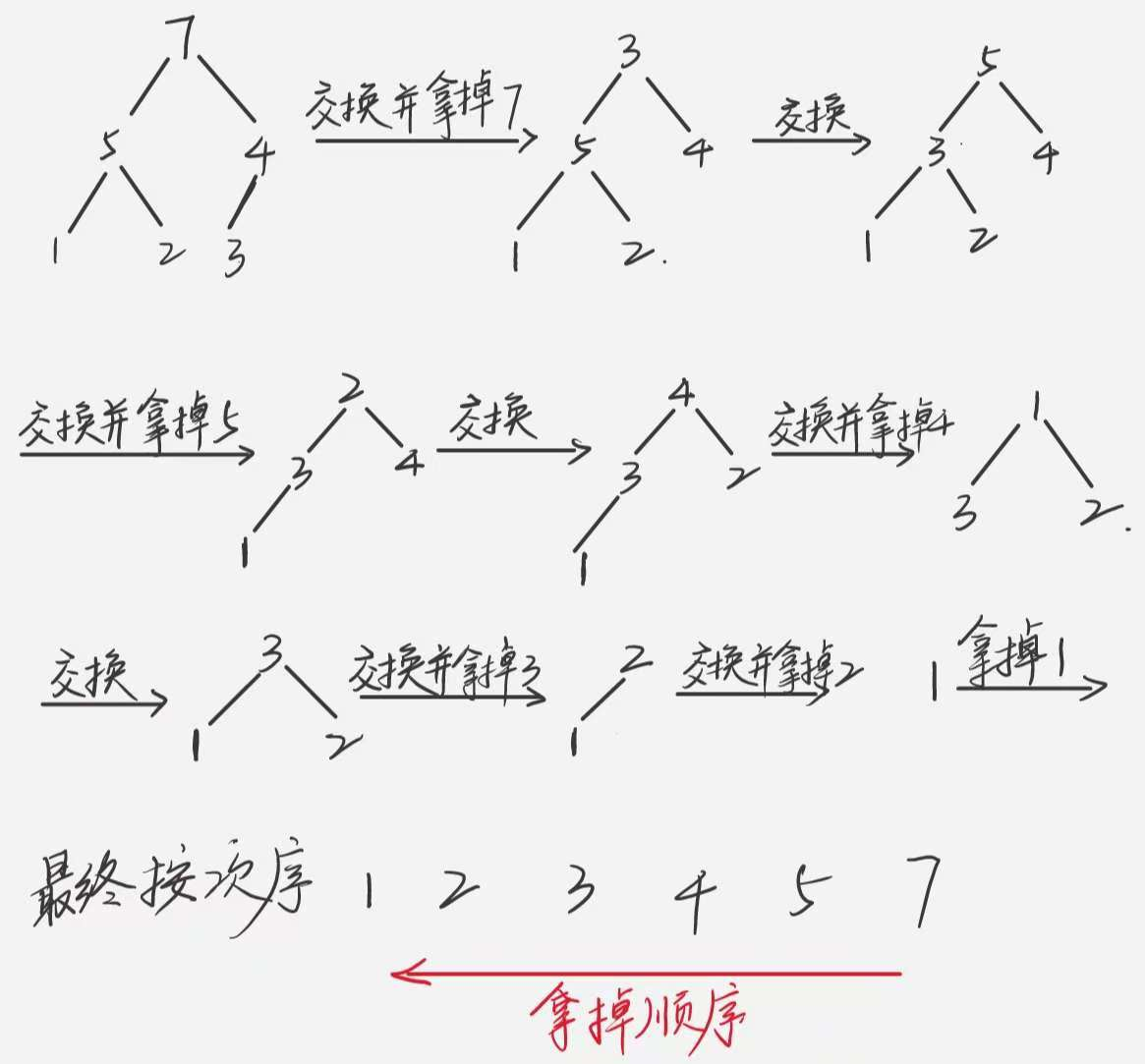
1、当我们从建堆中获得初始大根堆后，首先交换最后一位和根节点位置，然后把最后一位拿掉，也就是此时堆中根节点为3，整个堆只有5个数。

2、开始调整，从堆的根节点开始，与子节点中最大的一个节点比较，如果比最大的一个节点要小，跟该节点交换，以此类推，直到调整的位置不再有子节点或者该节点已经比最大的子节点还要大时，结束本次遍历。

3、此时，重新形成了大根堆，再次将根节点和最后一位交换位置，然后把最后一位拿掉。重新执行2。直到将堆全部拿掉为止。

4、最后你可以发现，你把拿掉的这些数按照先后次序排好序，就是从小到大的顺序排列的。

3、代码实现（C++）

void heapSort(vector<int>& arr) {
	
	if (arr.size() < 2 || arr.empty())
		return;

	for (int i = 0; i < arr.size(); i++) {
		heapInsert(arr, i); // 一个一个插，实现初始化大根堆
	}

	/*for (int i = arr.size()-1; i >= 0; i--) {
		heapify(arr, i, arr.size()); //从最后一个元素为根，使用heapify调整，并循环往前
	}*/

	int heapSize = arr.size();

	swap(arr, 0, --heapSize);//将大根堆根节点与最后一位交换位置，heapSize-1

	while (heapSize > 0)
	{
		heapify(arr, 0,heapSize); //从根节点开始，重新调整至大根堆
		swap(arr, 0, --heapSize);
	}
}

void heapInsert(vector<int>& arr, int index) {
	while (arr[(index - 1) / 2] < arr[index]) {
		swap(arr, (index - 1) / 2, index);
		index = (index - 1) / 2;
	}
}

void swap(vector<int>& arr, int i, int j)
{
	int temp = arr[i];
	arr[i] = arr[j];
	arr[j] = temp;
}

void heapify(vector<int>& arr, int root,int heapSize)
{
	int index = root;
	while (index * 2 + 1 < heapSize) //循环条件要求至少有一个子节点
	{
		//两个孩子中，谁的值更大，把下标给largest
		int largest = index*2+2 < heapSize && arr[index * 2 + 1] < arr[index * 2 + 2] ? index * 2 + 2 : index * 2 + 1;
		
		//父和较大孩子之间比较，父的大，退出；孩子大，交换
		if (arr[index] > arr[largest])
			break;
		swap(arr, index, largest);
		//更新父节点
		index = largest;
	}
}

4、时间复杂度分析

即heapSort()的时间复杂度：

（1）分析建堆过程，时间复杂度O(NlogN)，

（2）分析heapSort()内的while循环执行N次，每次都执行一次heapify()调整堆，调整堆的过程就是从根节点不断遍历到叶节点的过程，最坏情况就是遍历一个树的高度logN。

最后，时间复杂度是O(NlogN) + O(NlogN) => O(NlogN)